I have been playing for two weeks with a BOSS OS-2 overdrive/distortion pedal I found in ebay for repair. Repairing was easy, just needed some pots cleaning.

The concept is nice: there are two blended circuits:
- Overdrive, by asymmetrical soft clipping in the feedback loop of an operational amplifier, like most overdrives out there.
- Distortion by symmetrical hard clipping in the output of the other operational amplifier of the same chip.
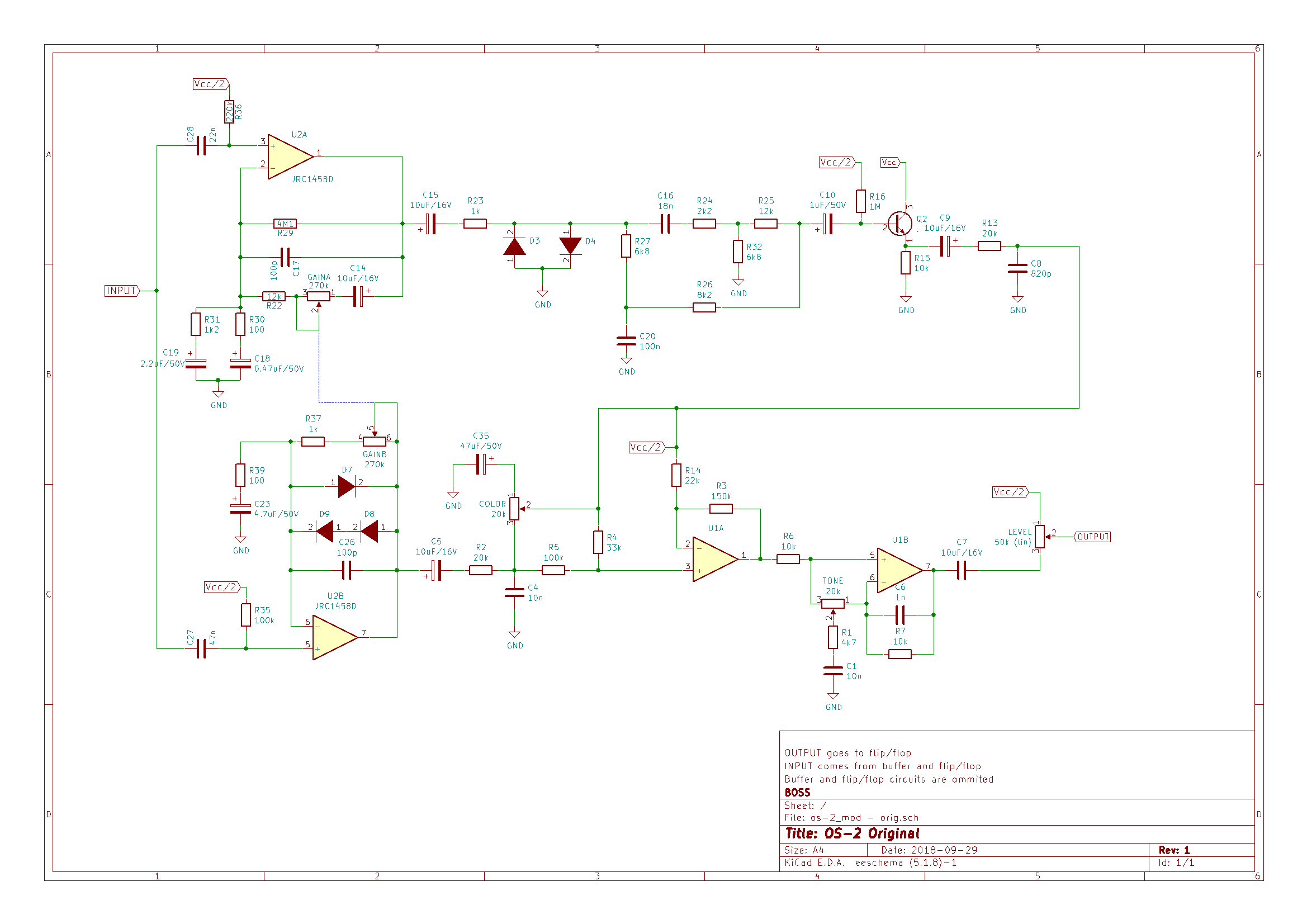
You can blend the two by rotating a “color” control, from overdrive on the left to distortion on the right. After the blend section, there is a tone one. The “Drive” pot is a dual 270k potentiometer, each unit connected to the feedback loop of each of the amplifier units.
Out of the brown box (it didn’t come with the original BOSS box) I found some things I didn’t like:
- Little bass response in the overdrive mode, too much treble for my liking. Usable for me, but could be improved (from my point of view, for my own needs).
- I usually don’t like pure distortions and hard clipping, so I didn’t expect to like this side too much. I found it too flat and hissing, with little mids, but having a nice boost in the 100Hz (aprox) freq.
I think there are almost no “bad designs” or “bad pedals” out there, it is just a matter of taste. Many like pedals that I hate (don’t want to give names). Maybe the best overdrive or distortion pedal is no pedal at all, but for people like me that usually don’t play on stadiums, distortion pedals are a good tool to get close to the tone of your favorite player.
Moreover, when you modify a pedal, you are not improving the design, but improving your particular unit for your particular taste. Most components vary a lot in value from unit to unit, and manufacturers have to take many constraints into consideration in their designs. Therefore I think we have to be humble when “improving” a device.
That said, in this case, I considered these objectives:
- Distortion side:
- Raising mids and cutting that hiss
- Trying asymmetrical clipping in this kind of circuits, just for fun
- Overdrive:
- Raising mids too, and add some more bass response
- Trying leds clipping for a supposedly more natural overdrive, and also for fun
After some tweaking and some regrets, I performed to the following changes:
| component | old value | new value | why |
| U2 (opamp) | JCR1458D | JCR4558D | JCR4558D has better characteristics: 1458D Input Resistance = 1M Slew Rate = 0,5V/uS4558: Input Resistance = 5M Slew Rate = 1V/uSSlew rate affects the circuit bandwidth higher limit, in this case from 8KHZ to 16KHz. Maybe it is overkill, but I think this gives more freedom at adjusting the frequency response of the circuit. |
| C6 | 1nF | 2n2F | Initially, I removed it but after Charles Willis suggestion, I replaced it for a 2.2nF capacitor. It should give more bass in the output of the tone stack. |
| C27 | 47nF | 220nF | Lowers freq. in high pass filter at the input of the overdrive section -> more bass |
| R39 | 100 | 150 | Lowers gain in overdrive. See C23 |
| C23 | 4.7uF | 2.2uF | In combination with R39, it forms a high pass filter, attenuating frequencies below the cut-off frequency. The modification changes the pass freq from 338Hz to 482Hz. In combination with the C27 change, it results in more mids |
| D7,D8,D9 | Junction diodes | D7,D8=Red LED – D9=BAT46 (Schottky) | It changes the form of the clipped signal. Red LEDs have Vf=1.8V (instead of 0,7) and different I/V curve. I put a schottky just to experiment, another kind of diode can be used, or just a cable for symmetrical clipping. Another LED would be too much Vf and can result in no clipping |
| R2 | 20K | 68K | This resistor is part of the circuit that balances overdrive and distortion. Since LEDs are used for clipping, the output voltage of the operational is too much when compared to distortion output. Raising the value of this resistor lowers the output of the overdrive section. R13 at the end of the distortion circuit can be lowered too, but that raises the cut-off frequency of the low pass filter formed by R13 and C8, not contributing to eliminate the hiss |
| C16 | 18nF | 22nF | Lowers the cut-off frequency of the high pass filter after the hard clipping section, raising mids in the overall circuit |
| D3,D4 | Junction diodes | D3=1N4148 – D4=BAT85 (Schottky) + 10 Ohms resistor | It changes the hard clipping section from symmetrical to asymmetrical. The schottky + resistor gives a smoother I/V curve than the diode alone. Just an experiment (successful for my ears), as in the soft clipping section |
| C8 | 820pF | 4.7nF | Lowers the cut-off frequency of the high pass filter after the hard clipping circuit. This is key to cut the hiss |

Lessons learned
At first I tried LEDs also in the hard clipping section, getting a not so nice result. Probing the circuit with the oscilloscope, I discovered that it was not clipping at all, you could remove the diodes and get the same output. Forward voltage is so high, even for red LEDs (different color LEDs have different Vf), that it didn’t clip at all. The distortion came from the saturated transistor and was not very pleasant.
Then I tried different combinations of Schottky and junction diodes (I like Schottky diodes lately…) until I got to the above blend.
I tried green and blue LEDs and combined LEDs with junction and Schottky in the soft clipping section, but I didn’t like the results. If you have read my other post about SD-1, green and schottky was my final combination in the BOSS SD-1, but it does not seem to work in the OS-2. The final combination was the nicer for my ears, just that.
I put a trimpot instead of R13, in order to adjust the output of the distortion circuit, but the result was catastrophic: more hiss and even oscillation when the trimpot got near zero ohms. So I changed R2, getting much better results.
As you can imagine, the values of the capacitors and resistance are not casual, I have tried many combinations and calculated some filter frequencies to get to those values. Some starting points came from forum posts and some other pages, and I changed some components and at the end returned to the original values (C26 for instance) . The lesson here is: calculate values for the filters involved and act with a purpose. I took some ideas from this post: https://www.roboticbeast.com/modification-de-la-boss-os-2/ but some didn’t wotk for me or with my unit. Another lesson (I already knew, of course) is that every modification affects the whole circuit in some measure, so you shouldn’t change a single component and see if you like it.
Also found a very useful tools for analyzing frequency responses by generating signals and capturing the output of the pedal with a computer and its sound card, more on this in some future post.
PD: if you make this mod, please comment below, I would like to keep track of people enjoying (or not) my mods.